Skip to contents

simulatr on your laptop

example-local.Rmd

Here we walk through a simple example of building a simulatr specifier object, checking and running the simulation locally, and visualizing the results. We consider estimating the coefficients in a linear regression model via ordinary least squares and lasso, varying the number of samples.

1. Assemble simulation components

  • parameter_grid. The problem parameters will be the sample size n, the dimension p, the number of nonzero coefficients s, and the value of each nonzero coefficient beta_val. In this simulation, we will only vary n. We could have therefore put the remainder of the parameters in fixed_parameters, but we avoid this to have all problem parameters in parameter_grid.

    parameter_grid <- data.frame(
  n = c(25, 50, 75, 100),      # sample size
  p = 15,                      # dimension
  s = 5,                       # number of nonzero coefficients
  beta_val = 3                 # value of nonzero coefficients
)

    Next, we want to create the ground truth inferential targets based on the problem parameters. In this case, the inferential target is the coefficient vector. We define a function get_ground_truth() that takes as input three of the problem parameters and outputs the coefficient vector:

    get_ground_truth <- function(p, s, beta_val){
  beta <- numeric(p)
  beta[1:s] <- beta_val
  list(beta = beta)
}

    We can append these ground truth inferential targets to parameter_grid using the helper function add_ground_truth():

    parameter_grid <- parameter_grid |> add_ground_truth(get_ground_truth)

    Let’s take a look at the resulting parameter grid:

    parameter_grid
#> # A tibble: 4 × 5
#>       n     p     s beta_val ground_truth    
#>   <dbl> <dbl> <dbl>    <dbl> <list>          
#> 1    25    15     5        3 <named list [1]>
#> 2    50    15     5        3 <named list [1]>
#> 3    75    15     5        3 <named list [1]>
#> 4   100    15     5        3 <named list [1]>

    We see the four columns with problem parameters and the fifth with the ground truth coefficient vectors.

  • fixed_parameters. Here we put only the number of data realizations B and the seed to set for the simulation.

    fixed_parameters <- list(
  B = 20,                      # number of data realizations
  seed = 4                    # seed to set prior to generating data and running methods
)

  • generate_data_function. We define the data-generation function as follows:

    # define data-generating model based on the Gaussian linear model
generate_data_f <- function(n, p, ground_truth){
  X <- matrix(rnorm(n*p), n, p, dimnames = list(NULL, paste0("X", 1:p)))
  y <- X %*% ground_truth$beta + rnorm(n)
  data <- list(X = X, y = y)
  data
}

    Note that we extract the coefficient vector beta from the ground_truth object. Additionally, we need to call simulatr_function() to add a few pieces of information that simulatr needs. In particular, we have to give it the argument names of the data-generating function (typically obtained using formalArgs(generate_data_f), as below). We also have to let simulatr know whether the data-generating function creates just one realization of the data (loop = TRUE) or all B at the same time (loop = FALSE).

    # need to call simulatr_function() to give simulatr a few more pieces of info
generate_data_function <- simulatr_function(
  f = generate_data_f,                        
  arg_names = formalArgs(generate_data_f),    
  loop = TRUE
)

  • run_method_functions. Let’s define functions for OLS and lasso:

    # ordinary least squares
ols_f <- function(data){
  X <- data$X
  y <- data$y
  lm_fit <- lm(y ~ X - 1)
  beta_hat <- coef(lm_fit)
  results <- list(beta = unname(beta_hat))
  results
}

# lasso
lasso_f <- function(data){
  X <- data$X
  y <- data$y
  glmnet_fit <- glmnet::cv.glmnet(x = X, y = y, nfolds = 5, intercept = FALSE)
  beta_hat <- glmnet::coef.glmnet(glmnet_fit, s = "lambda.1se")
  results <- list(beta = beta_hat[-1])
  results
}

    Again, we need to call simulatr_function() to add a few pieces of information that simulatr needs. This time, we need to give it all arguments to the method functions except the first (the data itself), which usually will be empty. We also have to let simulatr know whether the method functions input just one realization of the data (loop = TRUE) or all B at the same time (loop = FALSE).

    # create simulatr functions
ols_spec_f <- simulatr_function(f = ols_f, arg_names = character(0), loop = TRUE)
lasso_spec_f <- simulatr_function(f = lasso_f, arg_names = character(0), loop = TRUE)

    Finally, we collate the above method functions into a named list. It is crucial that the list be named.

    run_method_functions <- list(ols = ols_spec_f, lasso = lasso_spec_f)

  • evaluation_functions. Let’s evaluate the estimate of beta using the RMSE. To accomplish this, we define the following evaluation function:

    rmse <- function(output, ground_truth) {
  sqrt(sum((output$beta - ground_truth$beta)^2))
}
evaluation_functions <- list(rmse = rmse)

2. Create a simulatr specifier object

This is the easiest step; just pass all four of the above components to the function simulatr_specifier():

simulatr_spec <- simulatr_specifier(
  parameter_grid,
  fixed_parameters,
  generate_data_function, 
  run_method_functions,
  evaluation_functions
)

3. Check and, if necessary, update the simulatr specifier object 

check_results <- check_simulatr_specifier_object(simulatr_spec, B_in = 2)
#> Generating data...
#> Running method 'ols'...
#> Running method 'lasso'...
#> 
#> SUMMARY: The simulatr specifier object is specified correctly!

This message tells us that the simulation did not encounter any errors for the first two data realizations. We are free to move on to running the full simulation.

4. Run the simulation on your laptop

Since this example simulation is small, we can run it on your laptop in RStudio:

sim_results <- check_simulatr_specifier_object(simulatr_spec)
#> Generating data...
#> Running method 'ols'...
#> Running method 'lasso'...
#> 
#> SUMMARY: The simulatr specifier object is specified correctly!

5. Summarize and/or visualize the results

Let’s take a look at the results:

sim_results$metrics
#> # A tibble: 8 × 8
#>   method metric  mean     se     n     p     s beta_val
#>   <chr>  <chr>  <dbl>  <dbl> <dbl> <dbl> <dbl>    <dbl>
#> 1 lasso  rmse   0.919 0.0711    25    15     5        3
#> 2 ols    rmse   1.24  0.0644    25    15     5        3
#> 3 lasso  rmse   0.593 0.0382    50    15     5        3
#> 4 ols    rmse   0.667 0.0327    50    15     5        3
#> 5 lasso  rmse   0.533 0.0289    75    15     5        3
#> 6 ols    rmse   0.482 0.0243    75    15     5        3
#> 7 lasso  rmse   0.467 0.0239   100    15     5        3
#> 8 ols    rmse   0.392 0.0237   100    15     5        3

We have both the mean and Monte Carlo standard error for the metric (RMSE) for each method in each problem setting. We can plot these as follows:

sim_results$metrics |>
  ggplot(aes(x = n, 
             y = mean, 
             ymin = mean - 2*se, 
             ymax = mean + 2*se, 
             color = method)) +
  geom_point() + 
  geom_line() + 
  geom_errorbar(width = 1) +
  labs(x = "Sample size",
       y = "RMSE") + 
  theme(legend.position = "bottom")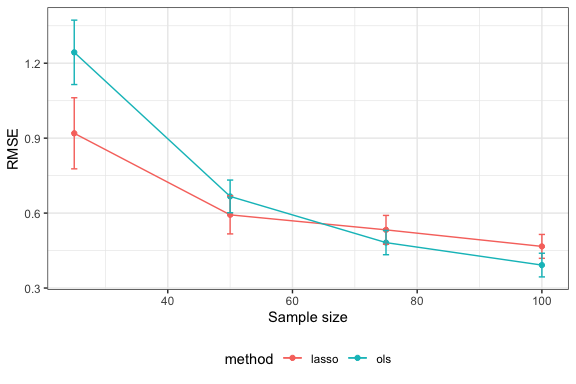

It looks like lasso performs better for small sample sizes but OLS performs better for large sample sizes.